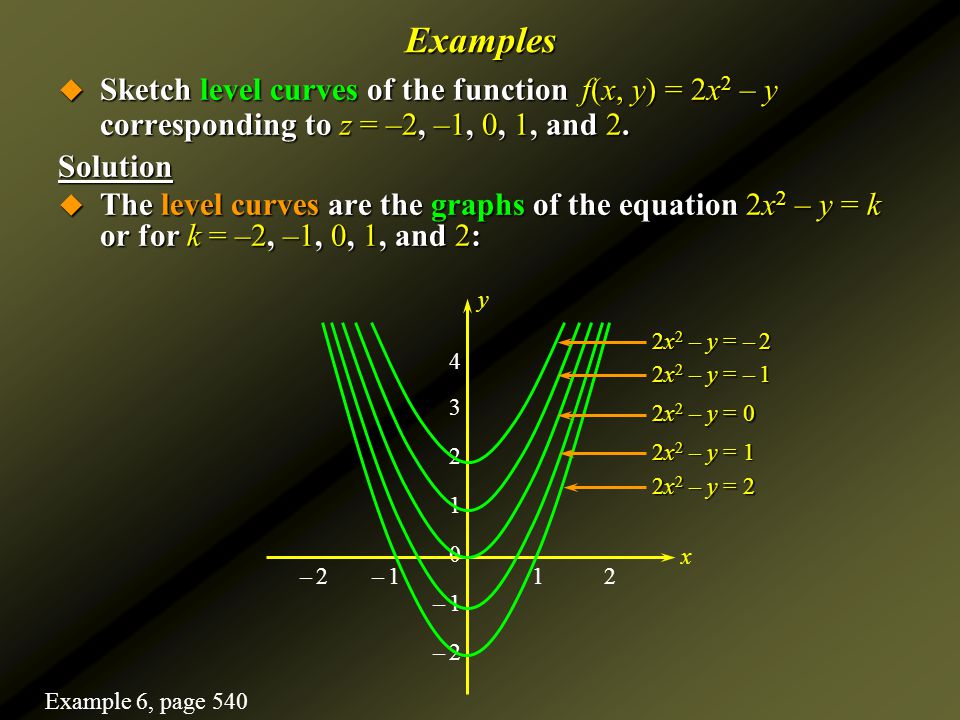
When the level curves are spaced far apart (in the center), there is a gradual change in the function values When the level curves are close together (near c = 5), there is a steep change in the function values 25 Example 7 Sketch a contour map of the function, using the level curves at c = 0, 2, 4, 6 and 8I've a plot of a 3D function of 2 variables and I'm interested into extrapolating the curve that I would like to obtain the level curves of a given function z=f(x,y) without using the countours function in the Matlab environment By letting Z equal to some constant 'c' we get a single level curve I would like to obtain an expression of the resulting function of the form y=f(x) to be able to study other properties of it Basic Example 1 Easy game
Http Math Msu Edu Gnagy Teaching 11 Fall Mth234 L12 234 Pdf
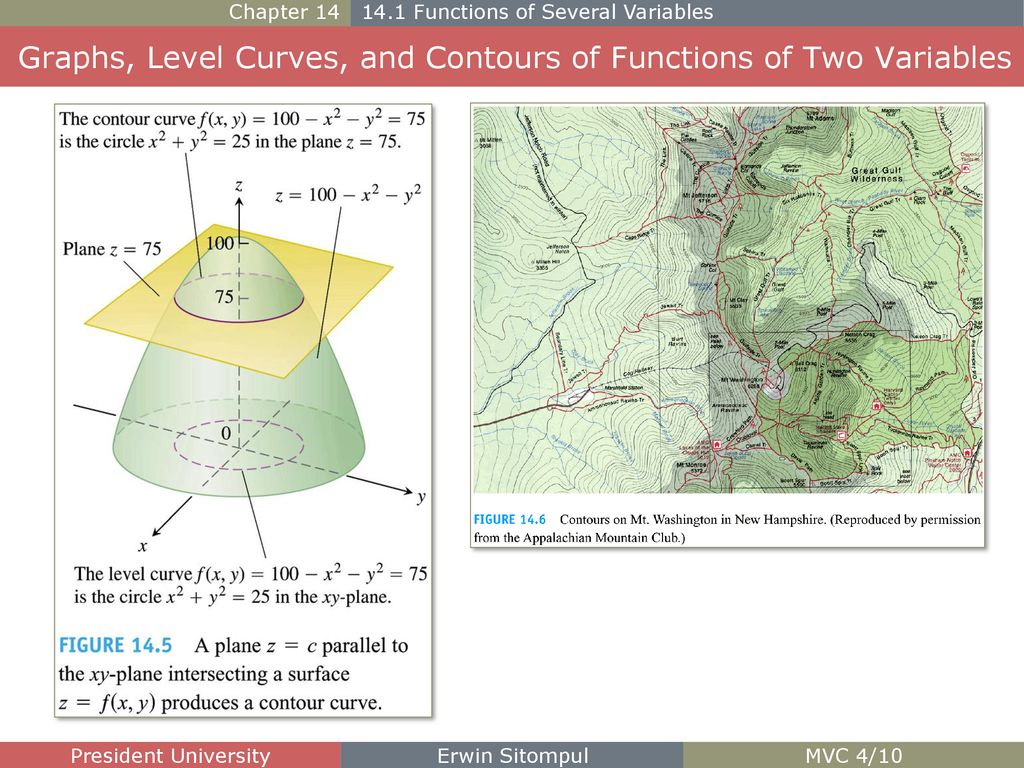
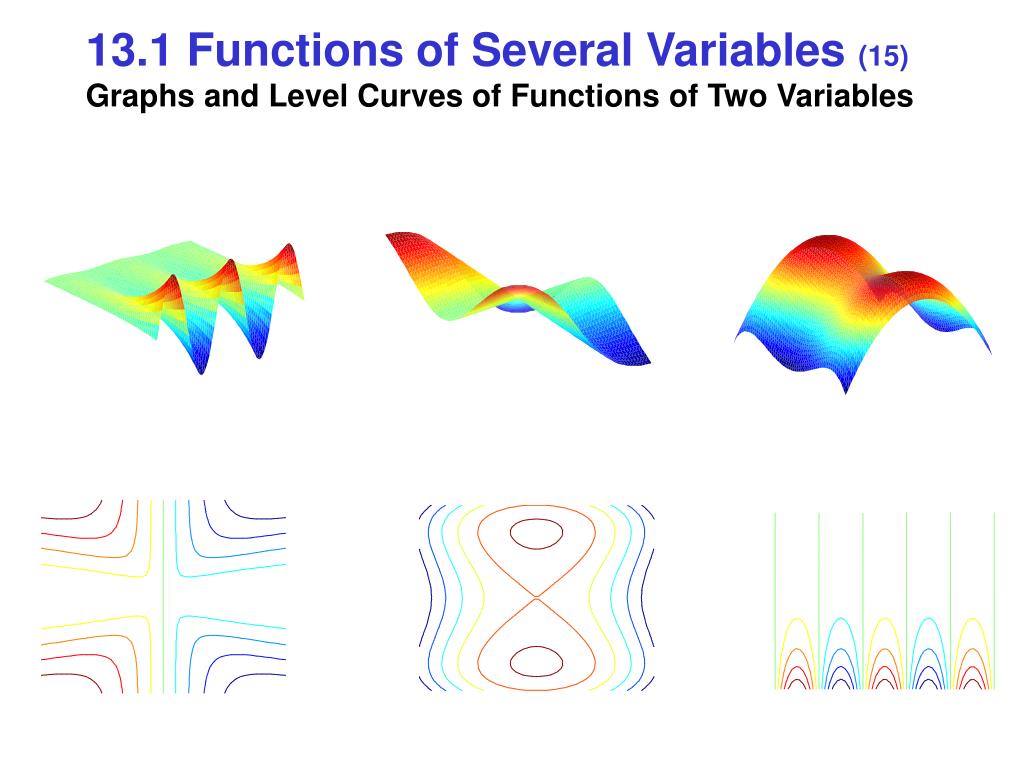
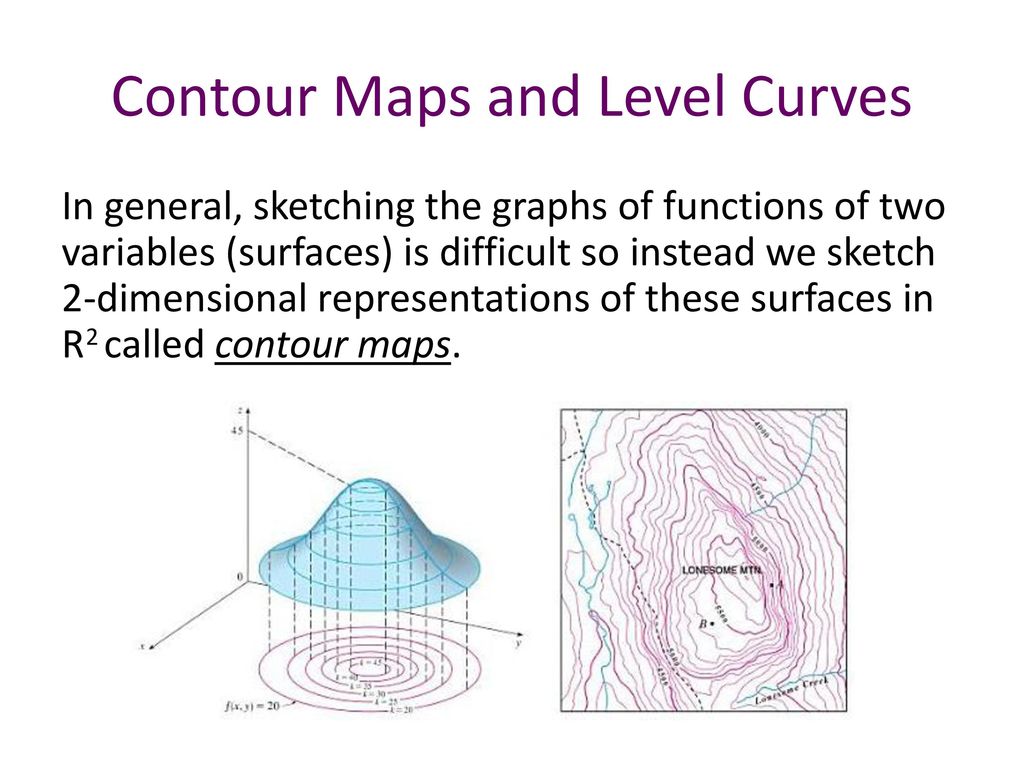
Graphs and level curves of functions of two variables
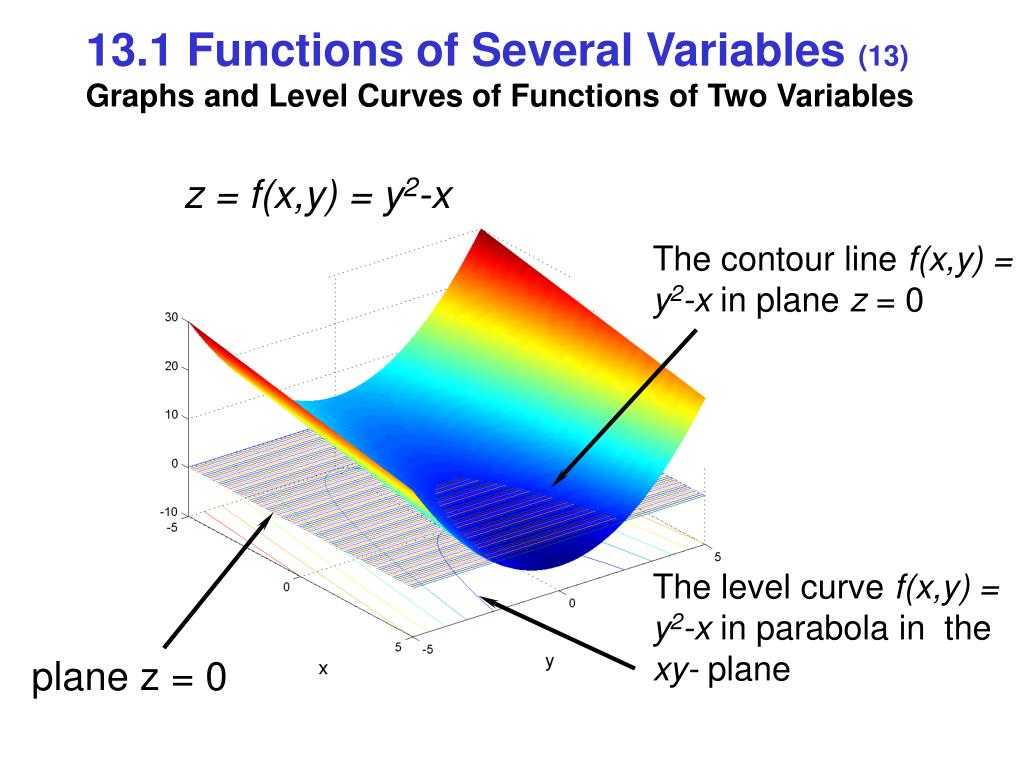
Graphs and level curves of functions of two variables-Def If f is a function of two variables with domain D, then the graph of f is {(x,y,z) ∈ R3 z = f(x,y) } for (x,y) ∈ D Def The level curves of a function f(x,y)are the curves in the plane with equations f(x,y)= kwhere is a constant in the range of f The contour curves are the correspondingFollow 2 views (last 30 days) Show older comments Giuseppe on Vote 0 ⋮ Vote 0 Edited Matt J on Accepted Answer Matt J Hi guys!



1
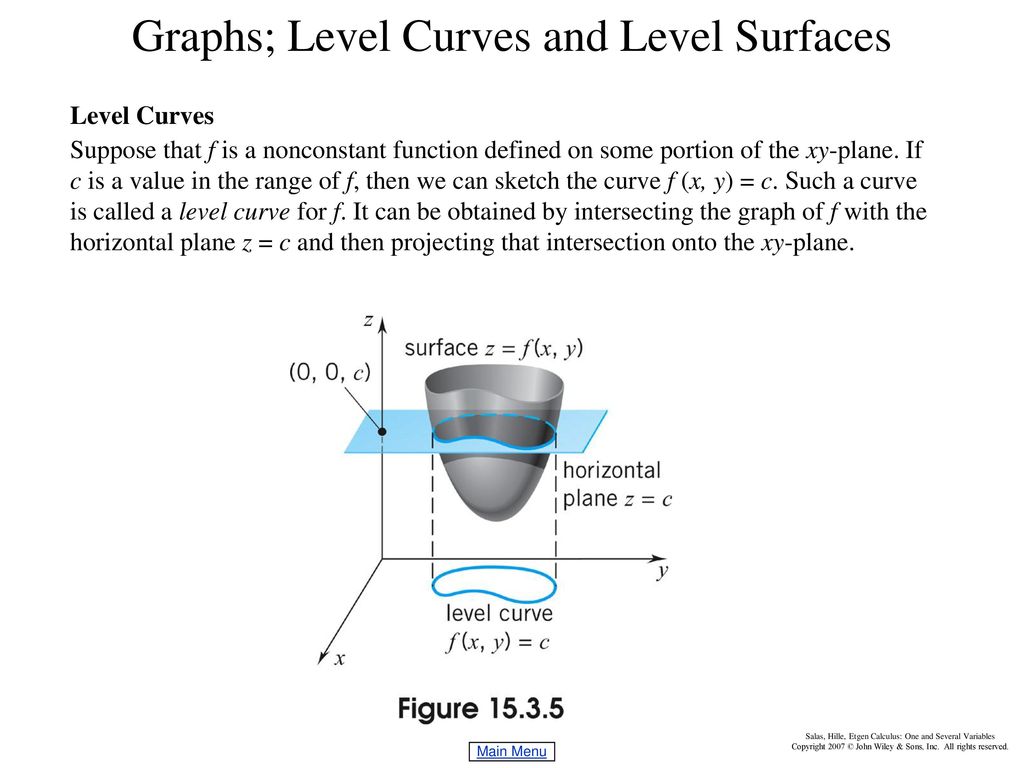
C Graph the level curve AHe, iL=3, and describe the relationship between e and i in this case T 37 Electric potential function The electric potential function for two positive charges, one at H0, 1L with twice the strength as the charge at H0, 1L, is given by fHx, yL= 2 x2 Hy1L2 1 x2 Hy 1L2 a Graph the electric potential using the window @5, 5Dµ@5, 5Dµ@0, 10 DLevel Curves and Contour Maps The level curves of a function f(x;y) of two variables are the curves with equations f(x;y) = k, where kis a constant (in the range of f) A graph consisting of several level curves is called a contour map Level Surfaces The level surfaces of a function f(x;y;z) of three variables are the surfacesFunctions of two variables have level curves, which are shown as curves in the x yplane x yplane However, when the function has three variables, the curves become surfaces, so we can define level surfaces for functions of three variables
Section 125 Functions of Three Variables Representing a Function of Three Variables using a Family of Level Surfaces Just as we could plot a family of level curves (a contour diagram) for a function f(x;y) of two variables, we can \plot" a family of level surfaces for a function of three variables w = f(x;y;z)One primary difference, however, is that the graphs of functions of more than two variables cannot be visualized directly, since they have dimension greater than three However, we can still use slice curves, slice surfaces, contours, and level sets to examine these higherdimension functions Definition level curves Given a function f(x, y) and a number c in the range of f, a level curve of a function of two variables for the value c is defined to be the set of points satisfying the equation f(x, y) = c Returning to the function g(x, y) = √9 − x2 − y2, we can determine the level curves of this function
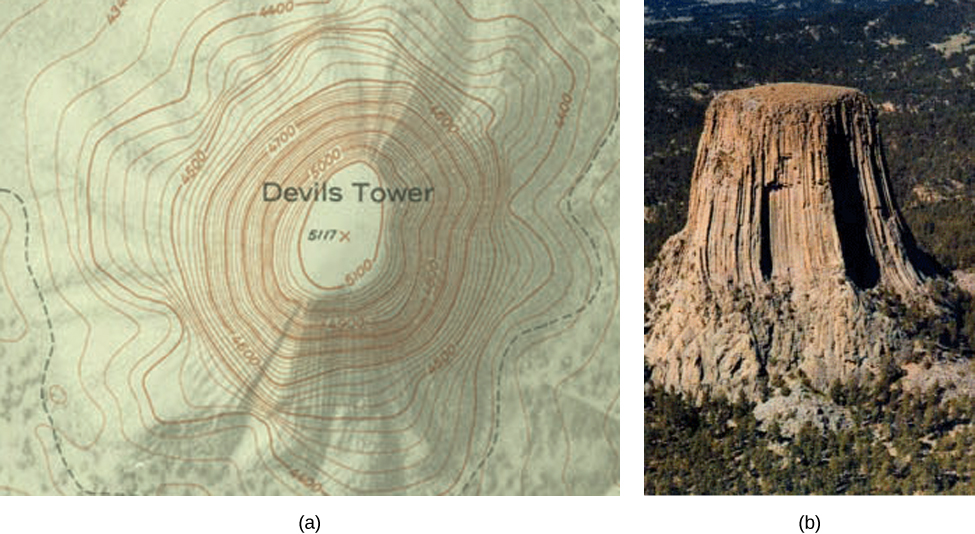
Level Surfaces It is very difficult to produce a meaningful graph of a function of three variables A function of one variable is a curve drawn in 2 dimensions; A level curve (or contour) of a function \(f\) of two independent variables \(x\) and \(y\) is a curve of the form \(k = f(x, y)\), where \(k\) is a constant Topographical maps can be used to create a threedimensional surface from the twodimensional contours or level curves19 Level Curves A second way to visualize a function of two variables is to use a scalar field in which the scalar z = f(x, y) is assigned to the point (x, y)A scalar field can be characterized by level curves (or contour lines) along which the value of f(x, y) is constant For instance, the weather map




3 Points Writing Prompt 1 Typed 100 0 Words In Chegg Com
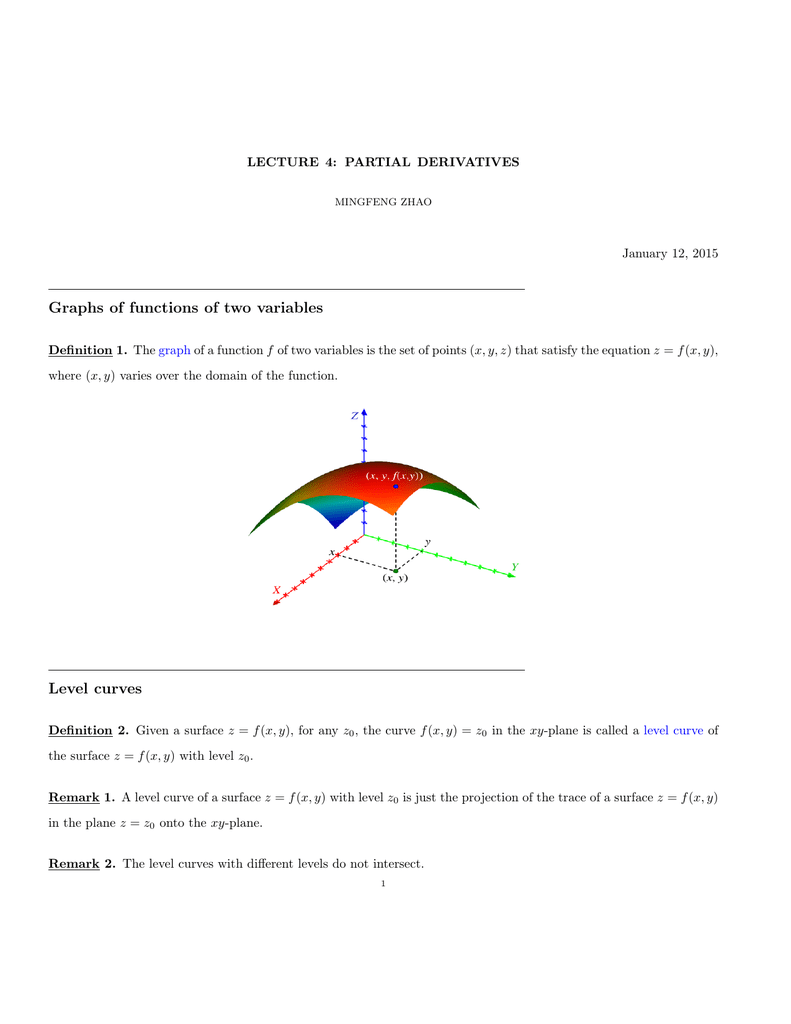



Graphs Of Functions Of Two Variables
When we talk about the graph of a function with two variables defined on a subset D of the xyplane, we mean zfxy xy D= (, ) ,( )∈ If c is a value in the range of f then we can sketch the curve f(x,y) = cThis is called a level curve A collection of level curves can give a good representation of the 3d graphTranscribed image text CURRENT OBJECTIVE Find the level curves of a function of two variables Question Choose the most specific description for the level curve of the function g(1,y) = zhy corresponding to c= 2 Select the correct answer below a line passing through the origin, excluding the origin a line passing through the origin O parabola ellipseThe level curves are The graph of a two variable function in 3D A set of curves tangent to the gradient of a function O A set of plane curves that describe a contour map of a graph in 3D A space curve in 3D fullscreen check_circle



0 3 Visualizing Functions Of Several Variables
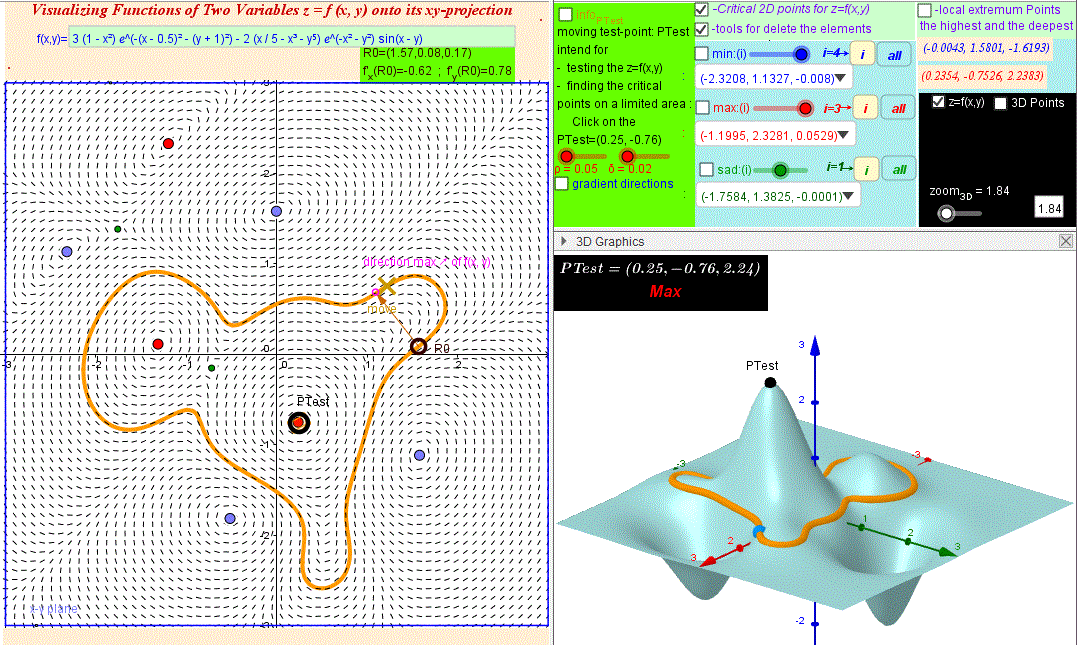



Visualizing Functions Of Two Variables Geogebra
Follow 1 view (last 30 days) Show older comments Giuseppe on Vote 0 ⋮ Vote 0 Edited Matt J on Accepted Answer Matt J Hi guys!Definition The level curves of a function f of two variables are the curves with equations f (x,y) = k, where k is a constant (in the range of f ) A level curve f (x,y) = k is the set of all points in the domain of f at which f takes on a given value k In other words, it shows where the graph of f has height k What we want to be able to do is slice through the figure at all different heights in order to get what we call the "level curves" of a function Then we want to be able to transfer all those twodimensional curves into the twodimensional plane, sketching those in the xyplane This will give us the sketch of level curves of the function



0 3 Visualizing Functions Of Several Variables



Functions Of Several Variables
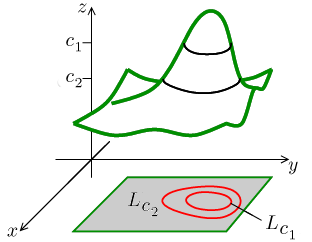
As in this example, the points (x, y) such that f (x, y) = k usually form a curve, called a level curve of the function A graph of some level curves can give a good idea of the shape of the surface;Picturing f(x;y) Contour Diagrams (Level Curves) We saw earlier how to sketch surfaces in three dimensions However, this is not always easy to do, or to interpret A contour diagram is a second option for picturing a function of two variables Suppose a function h(x;y) gives the height above sea level at the point (x;y) on a map Here is a set of practice problems to accompany the Functions of Several Variables section of the 3Dimensional Space chapter of the notes for Paul Dawkins Calculus III course at Lamar University 7 identify and sketch the level curves (or contours) for the given function \(2x 3y {z^2} = 1\) Solution \(4z 2{y^2} x = 0\) Solution



Http Math Msu Edu Gnagy Teaching 11 Fall Mth234 L12 234 Pdf




Ppt Chapter 14 Partial Derivatives Powerpoint Presentation Free Download Id
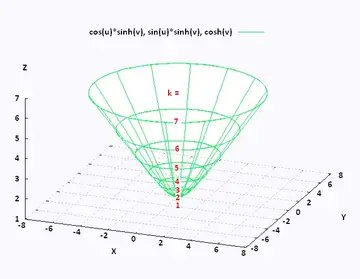
How to extrapolate a level curve form a 3D plot of a 2variables function?X y 143 Level Curves and Level Surfaces Look over book examples!!!It looks much like a topographic map of the surface In figure 1412 both the surface and its associated level curves are shown



Http Mathcs Holycross Edu Groberts Courses Ma241 Classroom Ch11 Functions Pdf




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
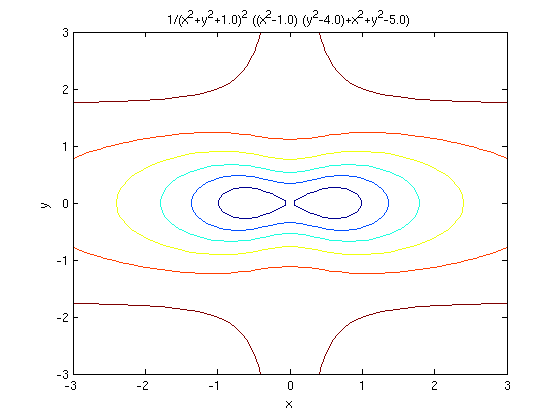
The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any number So the equations of the level curves are \(f\left( {x,y} \right) = k\) Note that sometimes the equation will be in the form \(f\left( {x,y,z} \right) = 0\) and in these cases the equations of the level curves are \(f\left( {x,y,k} \right) = 0\)In weather maps of atmospheric pressure at a given timeas a function of longitude and latitude, the level curves arecalled isobars and join locations with the same pressureSurface winds tend to flow from areas of high pressureacross the isobars toward areas of low pressure, and arestrongest where the isobars are tightly packed112 Contours and level curves Three dimensional surfaces can be depicted in two–dimensions by means of level curves or contour maps If f DˆR2!R is a function of two variables, the level curves of f are the subsets of D f(x;y) 2D f(x;y) = cg;
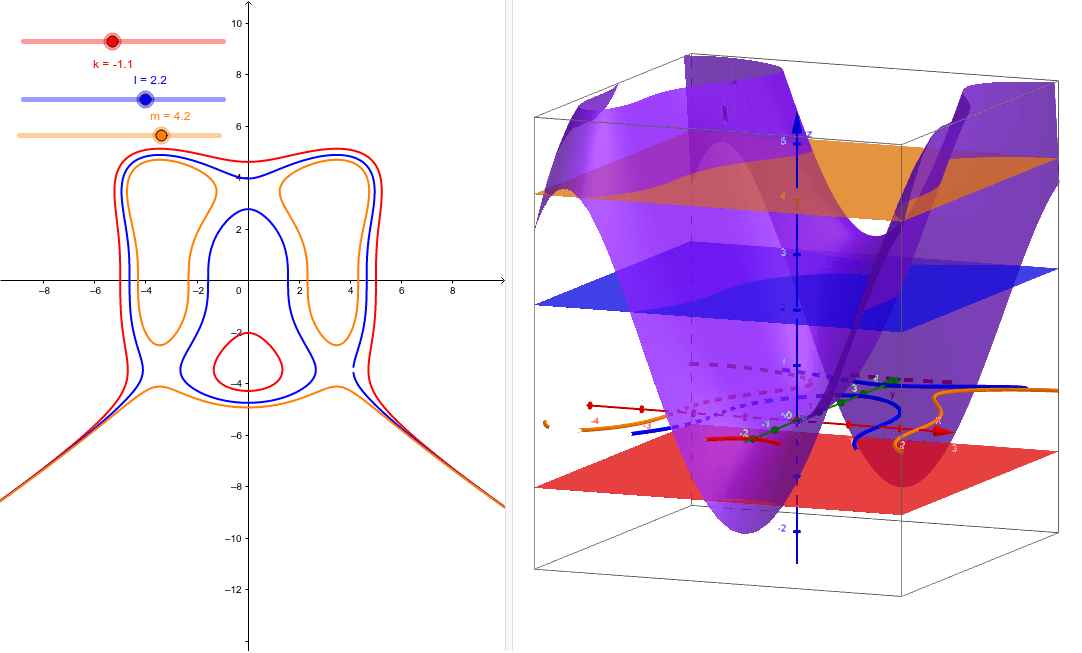



Function Of Several Variables Several Level Curves Geogebra




Calculus Iii Functions Of Several Variables
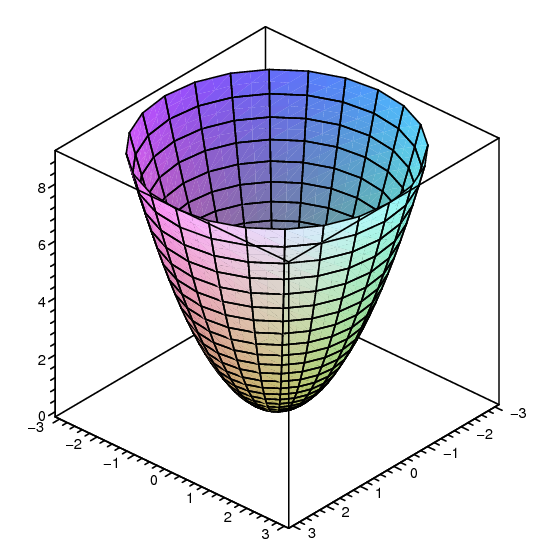
I've a plot of a 3D function of 2 variables and I'm interested into extrapolating the curve that corresponds How to extrapolate a level curve form a 3D plot of a 2variables function?Recall that the graph of a function f of one variable is the curve y = f(x) in an xyplane consisting of the points (x,y) with x in the domain of the function and y = f(x) The graph of a function of two variables is a surface in threedimensional space 270 Section 141, Functions of two variables p




Level Curves Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
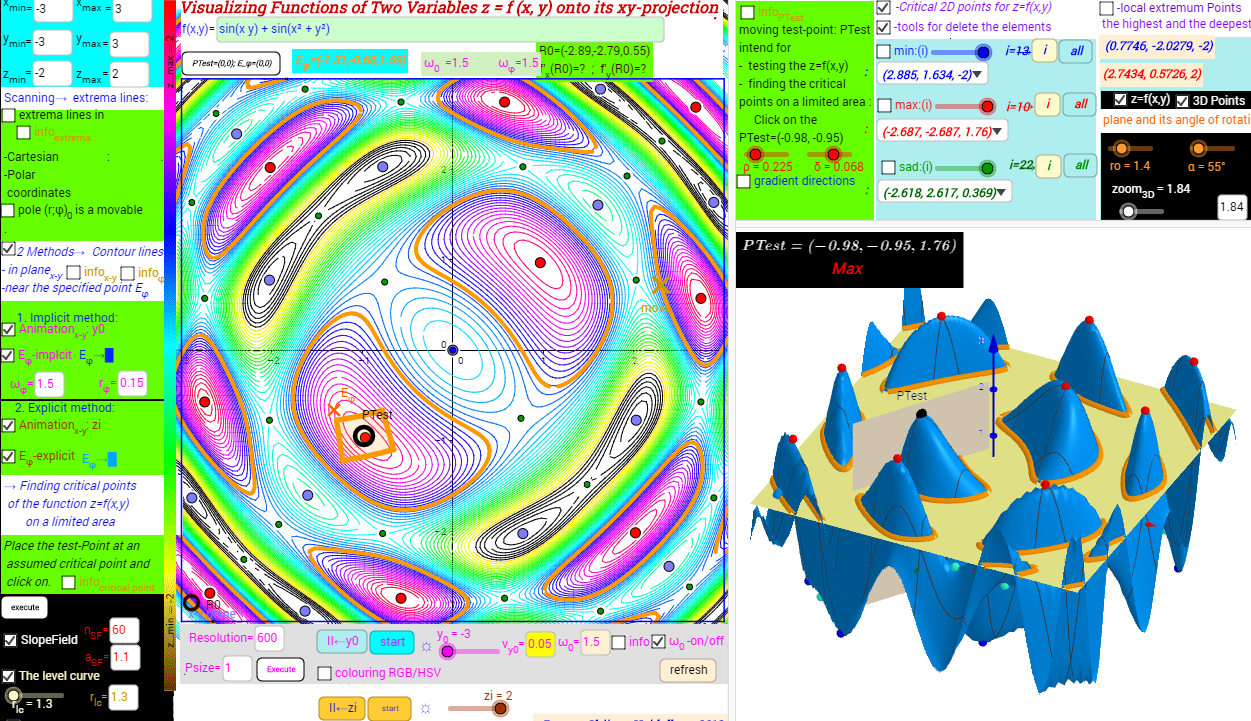



Sin X Y Sin X 2 Y 2 Images To Visualizing Functions Of Two Variables Geogebra
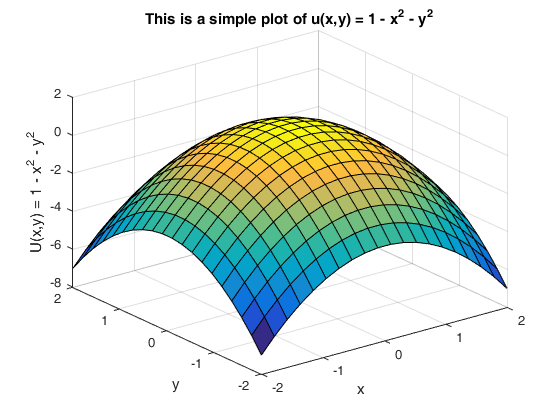
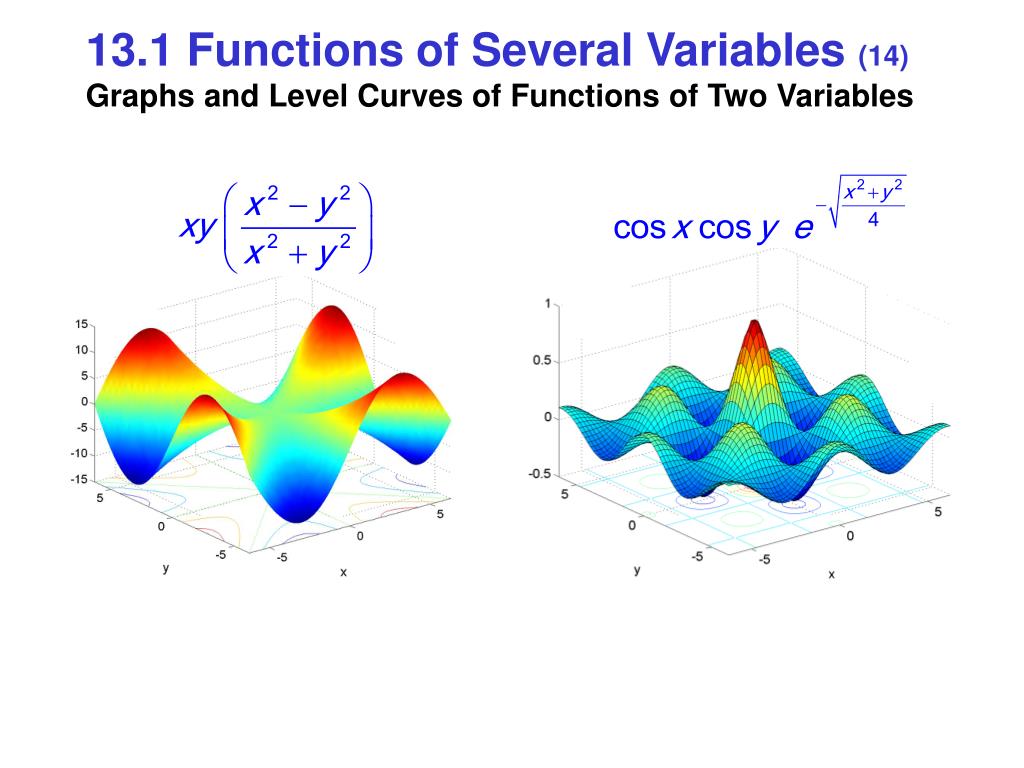
So level curves, level curves for the function z equals x squared plus y squared, these are just circles in the xyplane And if we're being careful and if we take the convention that our level curves are evenly spaced in the zplane, then these are going to get closer and closer together, and we'll see in a minute where that's coming fromCalculus Integral with adjustable bounds example Calculus Fundamental Theorem of CalculusGiven a function f(x,y), the set f(x,y) = c = const is called a contour curve or level curve of f For example, for f(x,y) = 4x2 3y2 the level curves f = c are ellipses if c > 0 Level curves allow to visualize functions of two variables f(x,y) Example For f(x,y) = x2 − y2 the set x2 − y2 = 0 is the union of the lines x = y and x = −y




13 1 Functions Of Several Variables Mathematics Libretexts




14 Partial Derivatives Copyright Cengage Learning All Rights
(1) We can write the surface as a level surface f(x, y, z) = c of a function of three variables, f(x, y, z) (2) We can parameterize the surface by writing x, y, and z each as functions of two parameters, say s and t This is analogous to parameterizing a curve and writing x, y, and z each as a functionDef A function z = f(x,y) of 2 variables x,y is a rule that assigns to each pair (x,y) a single value for z x,y are independent variables while z is a dependent variable The domain is a subset of Def The level curves of a function f of two variables are the curves with equations f(x,y) = k, where k is a constant (in the range of f)Where c=constant If f= height, level curves are contours on a contour map If f= air pressure




Level Set Wikipedia




Level Set Wikipedia
I Functions of two variables I Graph of the function I Level curves, contour curves I Functions of three variables I Level surfaces On open and closed sets in Rn We first generalize from R3 to Rn the definition of a ball of radius r centered at Pˆ Definition A set B r (Pˆ) ⊂ Rn, with n ∈ N and r > 0, is a ball of radius r(a) The level curves of a function of two variables are specified as f(x,y) =const Express the derivative of this function at any point (x,y) in terms of the partial derivatives of f(x,y) Draw some level curves of the real and imaginary parts of the function w = z'in the (x,y) planeThe Perpendicularity of The Gradient at a Point on a Level Curve Recall from The Gradient of Functions of Several Variables page that if is a two variable realvalued function whose first partial derivatives exist, then the gradient of is (1) We are now going to look at a very important theorem that says if is differentiable at some point on



Mathematics Calculus Iii




Chapter 14 Partial Derivatives Chapter 14 Partial Derivatives Ppt Download
Level Curves This worksheet illustrates the level curves of a function of two variables You may enter any function which is a polynomial in both andWhen the number of independent variables is two, a level set is called a level curve, also known as contour line or isoline;Differentiation of Functions of Several Variables Section 1 Functions of Several Variables Select Section 41 Functions of Several Variables 42 Limits and Continuity 43 Partial Derivatives 44 Tangent Planes and Linear Approximations 45 The Chain Rule 46 Directional Derivatives and the Gradient 47 Maxima/Minima Problems 48




Some Examples Of Graphs Used In The Problems A Level Curves Of A Download Scientific Diagram



1
One way to collapse the graph of a scalarvalued function of two variables into a twodimensional plot is through level curves A level curve of a function f (x, y) is the curve of points (x, y) where f (x, y) is some constant value A level curve is simply a cross section of the graph of z = f (x, y) taken at a constant value, say z = cIf we look for different values of f we get different curves (Eg f ( x, y) = 4 is a circle of radius 2 instead of 1) The third way to get a curve is to track the trajectory of a moving point If we specify both x and y as functions of a parameter t (time), then we get more than a geometric set We get a description of how the curve is being Check for values that make radicands negative or denominators equal to zero Functions of two variables have level curves, which are shown as curves in the However, when the function has three variables, the curves become surfaces, so we can define level surfaces for functions of three variables Definition



Chapter 14 Partial Derivatives Chapter 14 Partial Derivatives Ppt Download




Functions Of Two Variables Graph Of A Function
This website and its content is subject to our Terms and Conditions Tes Global Ltd is registered in England (Company No 0172) with its registered office at 26 Red Lion Square London WC1R 4HQFor a function of three variables f (x,y,z) the notion corresponding to the level curve of a twovariable function is a level surface, f (x,y,z)=c This is generally a surface, which can be plotted with the help of MapleMy Partial Derivatives course https//wwwkristakingmathcom/partialderivativescourseIn this video we're talking about how to sketch the level curves of




Level Set Wikipedia




Sketch Saddle Point Of A Function Of Two Variables F X Y 4 X 3 Y 3 3xy Stewart P930 Question 14 7 3 Mathematics Stack Exchange
Session 25 Level Curves and Contour Plots Part A Functions of Two Variables, Tangent Approximation and Optimization 2 Partial Derivatives Multivariable Calculus Mathematics MIT OpenCourseWare This session includes a lecture video clip, board notes, course notes, examples, two recitation videos, and a MathletAnother example is the two variable realvalued function $f(x, y) = x^2 y^2$ which represents a hyperboloid The level curves generated by the planes $z = 1$, $zSo a level surface is the set of all realvalued roots of an equation in three variables x 1, x 2 and x 3




In Calculus I And Ii We Worked With Functions Chegg Com



1
A function of two variables is a surface drawn in 3 dimensions;A function of three variables is a hypersurface drawn in 4 dimensionsExample 7 Describe the level curves of the function f(x,y) = x2 y2 from Examples 2 and 3 Answer Figure a shows horizontal cross sections of the graph of f and Figure b shows the corresponding level curves • The level curve f = c is the circle of radius √ c with its center at the origin if c > 0, is the origin if x = 0, and is empty



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework13 1 Ans Pdf



Draw Level Curves For Functions Of Two Variables In C C Helper
A level curve (or contour) of a function \(f\) of two independent variables \(x\) and \(y\) is a curve of the form \(k = f(x,y)\text{,}\) where \(k\) is a constant Topographical maps can be used to create a threedimensional surface from the twodimensional contours or level curvesSo a level curve is the set of all realvalued solutions of an equation in two variables x 1 and x 2 When n = 3, a level set is called a level surface (or isosurface);




16 1 Functions Of Several Variables
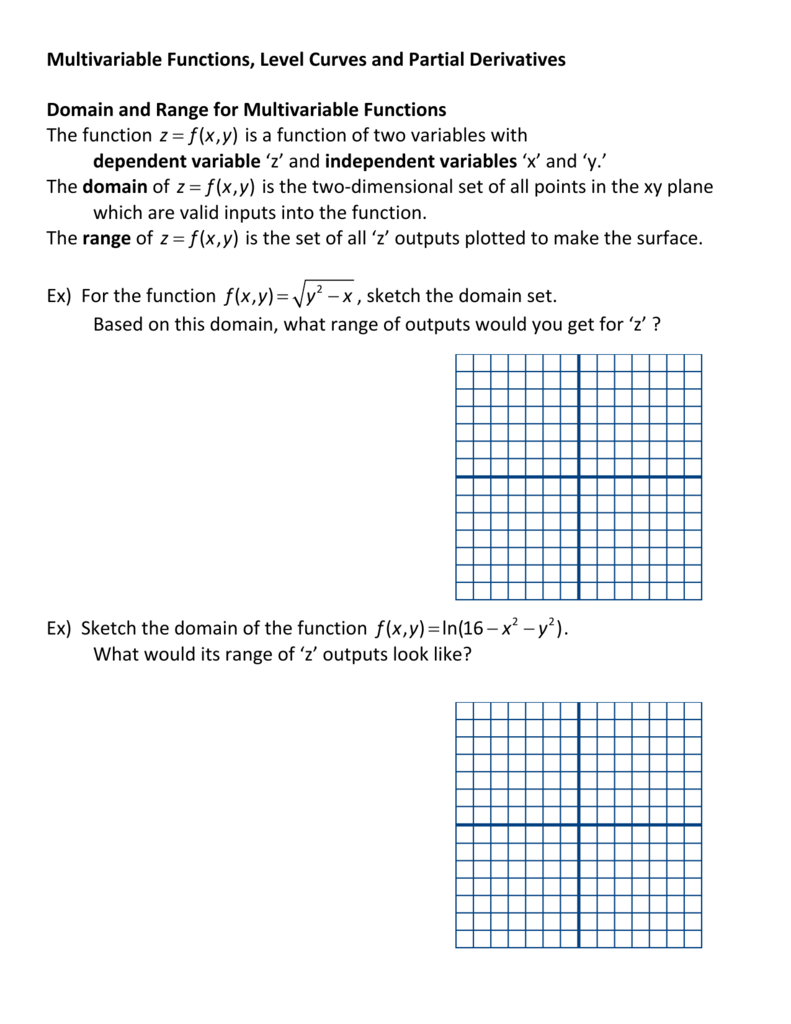



Multivariable Functions Level Curves And Partial Derivatives



Calculus Iii Functions Of Several Variables




Level Curves Of Functions Of Two Variables Youtube




How Do You Sketch Level Curves Of Multivariable Functions Youtube
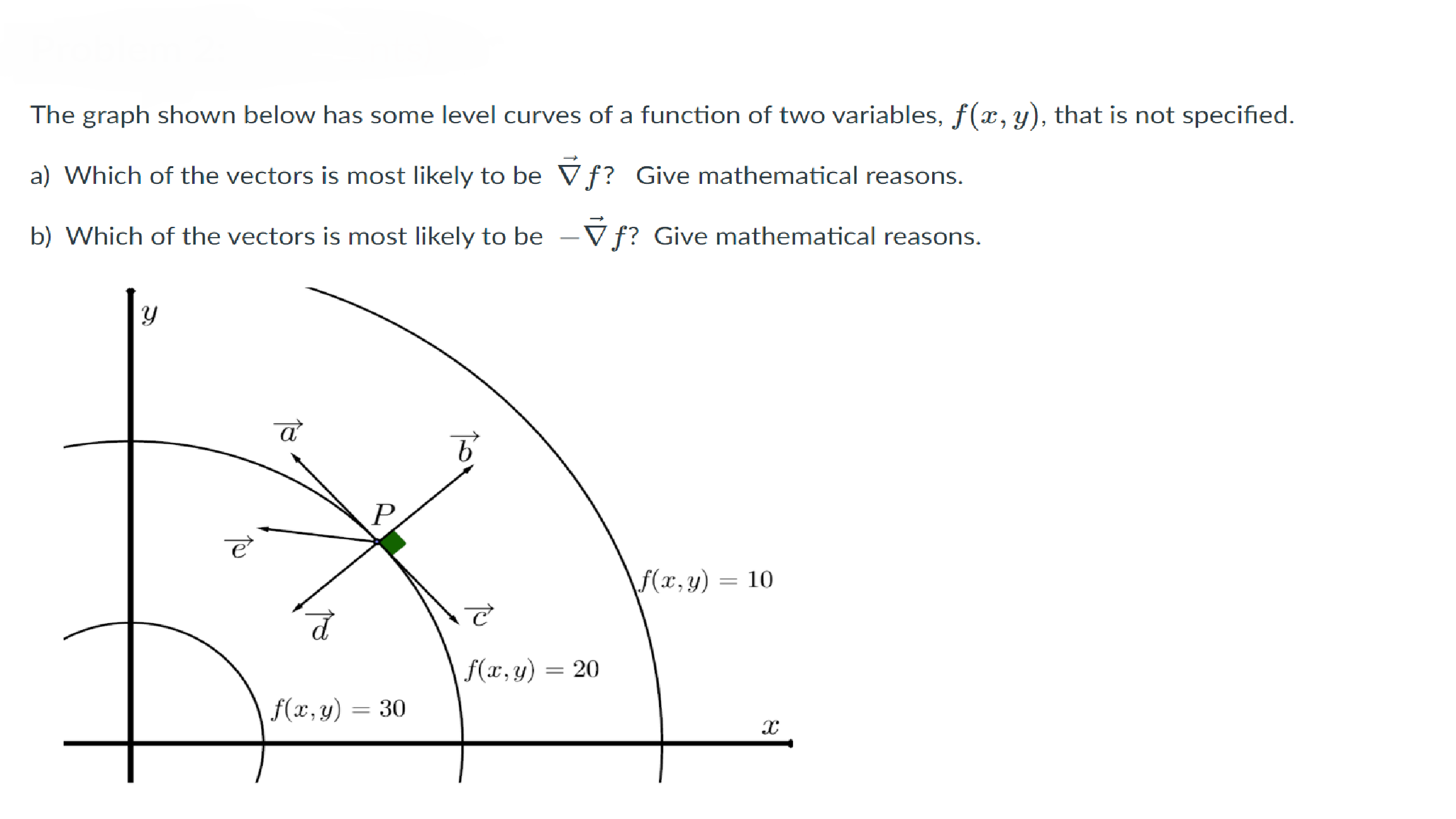



The Graph Shown Below Has Some Level Curves Of A Chegg Com



Howtoplotfunctiontwovariables



Level Curves Functions Of Several Variables By Openstax Page 3 12 Jobilize



1



0 3 Visualizing Functions Of Several Variables




Functions Of Two And Three Variables Level Curves Contours Level Surfaces Youtube




1 Let The Function Of Two Variables Be Given As A Chegg Com



Http Abel Math Harvard Edu Knill Teaching Summer14 Handouts Week2 Pdf



Lecture 4 Graph Level Curves Contour Lines Of Functions Of Two Variables Youtube



Math Tutor Extra Functions Of More Variables



Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id




8 Calculus Of Several Variables U Functions Of




Partial Derivatives 15 Partial Derivatives So Far We Have Dealt With The Calculus Of Functions Of A Single Variable However In The Real World Physical Ppt Download




Calculus Iii Functions Of Several Variables




Introduction To Functions Of Several Variables Ppt Download




Introduction To Functions Of Several Variables



Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id



Visualizing Functions Of Several Variables And Surfaces




How To Read Contour Plot Mathematics Stack Exchange



Www Usna Edu Users Oceano Raylee Sm223 Ch14 1 Stewart 16 Pdf



Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id



Solved Define The Level Curves Of A Function Of Two Variables Give Examples Of Several Surfaces Whose Level Curves Are Circles And At Least One Ex Course Hero




Level Curves




1 Objective Functions In Two Variables Partial Differentiation



Www Math Uci Edu Remote Teaching Lecture Notes Of Hamed Math 2d lecture notes Lecture note 14 1 Pdf




3 D Calculus Continuous Function Function Mathematics




Chapter 14 Partial Derivatives Chapter 14 Partial Derivatives Ppt Download




Calculus Iii Functions Of Several Variables




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



Labware Ma35 Multivariable Calculus Two Variable Calculus




Functions Of Two Variables Graph Of A Function




Level Curves




Level Set Wikipedia




Calculus Iii Functions Of Several Variables
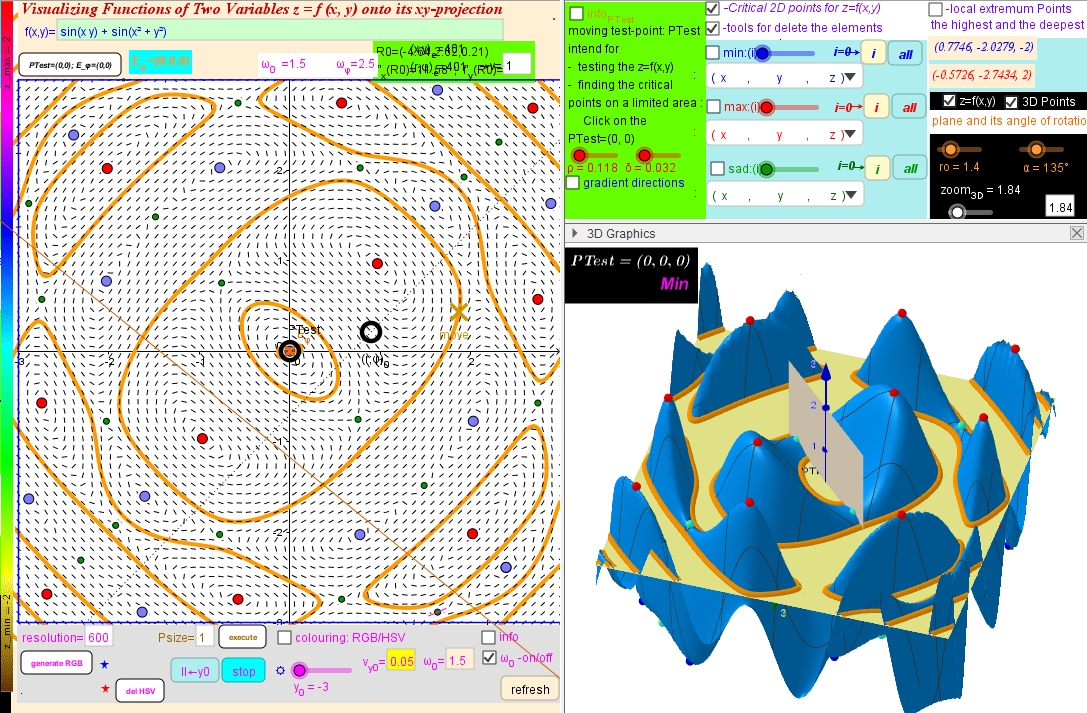



Sin X Y Sin X 2 Y 2 Images To Visualizing Functions Of Two Variables Geogebra



Http Diposit Ub Edu Dspace Bitstream 2445 1 Student E2 80 99s autonomous learning and tools for teachers by means of the use of geogebra 28 C3 81lvarez et al 18 29 Pdf
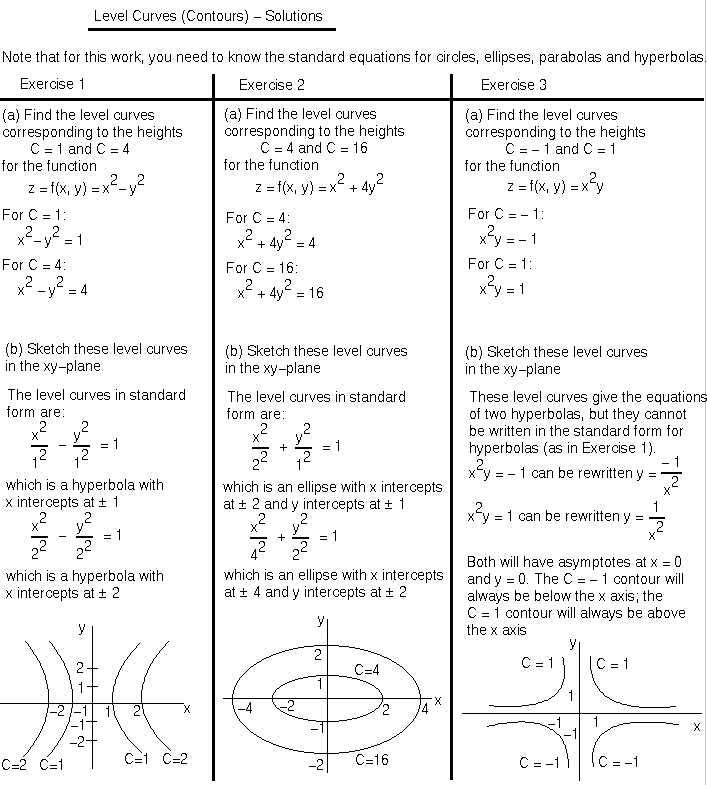



Functions Of Two Variables Math100 Revision Exercises Resources Mathematics And Statistics University Of Canterbury New Zealand
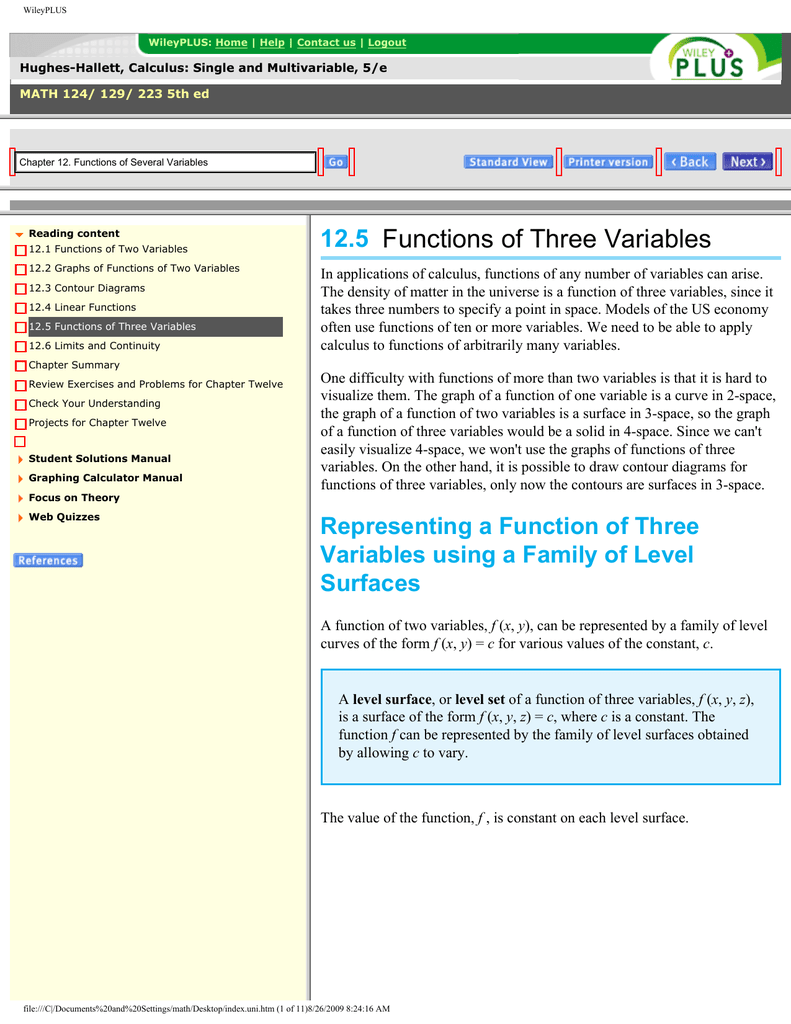



12 5 Functions Of Three Variables



Q Tbn And9gcsg2 Dp6eaxlk 1ytlb 7wqm97kz2m B 0bn1n7tp0tiijphv X Usqp Cau




Level Curves And Implicit Differentiation Studocu



8 Calculus Of Several Variables Functions Of Several Variables Ppt Download



Announcements Topics To Do Ppt Download




Level Sets Math Insight



Chapter 15 Functions Of Several Variables Ppt Download




Level Curves




Level Sets Math Insight



0 3 Visualizing Functions Of Several Variables




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




13 1 Functions Of Several Variables Mathematics Libretexts



0 3 Visualizing Functions Of Several Variables




Lecture Notes Chapter 1 1 Part2 Contourlines Level Curves And 3d Graphs Pdf



16 1 Functions Of Several Variables




Level Curves Calculus



Procedure For Computation Of The Goodness Of Fit Indicators Two Download Scientific Diagram




Presentation On Introduction To Several Variables And Partial Derivat




Multivariable Functions And Their Level Curves Dave4math



Functions Of Two Variables Lessons Blendspace
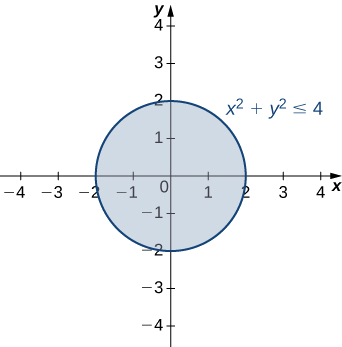



13 1 Functions Of Several Variables Mathematics Libretexts
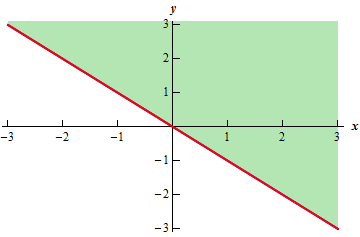



Calculus Iii Functions Of Several Variables



Www Usna Edu Users Oceano Raylee Sm223 Ch14 1 Stewart 16 Pdf




14 Partial Derivatives Copyright Cengage Learning All Rights
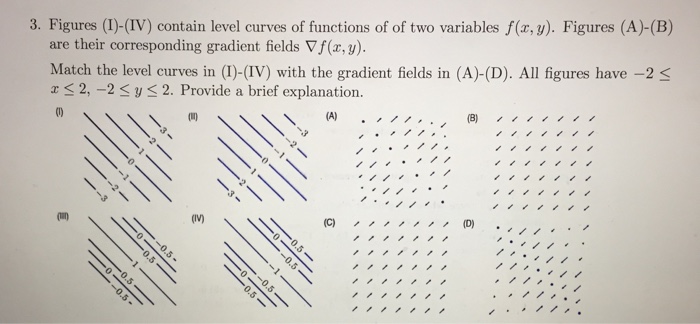



Figures I Iv Contain Level Curves Of Functions Of Chegg Com
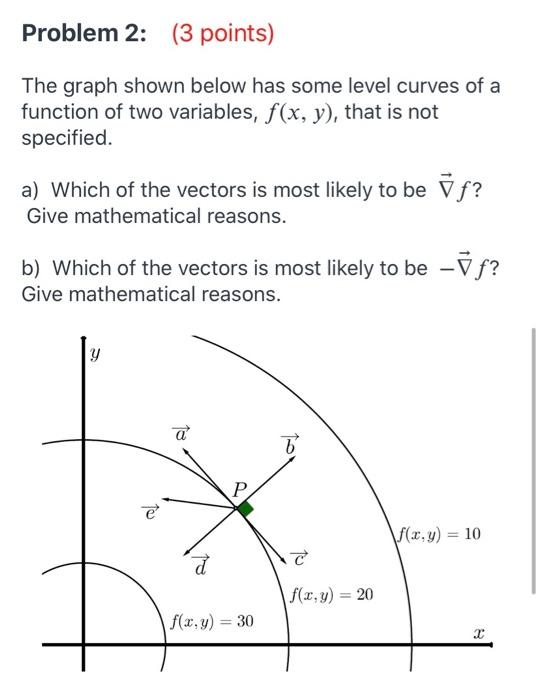



Problem 2 3 Points The Graph Shown Below Has Some Chegg Com




Level Sets Math Insight
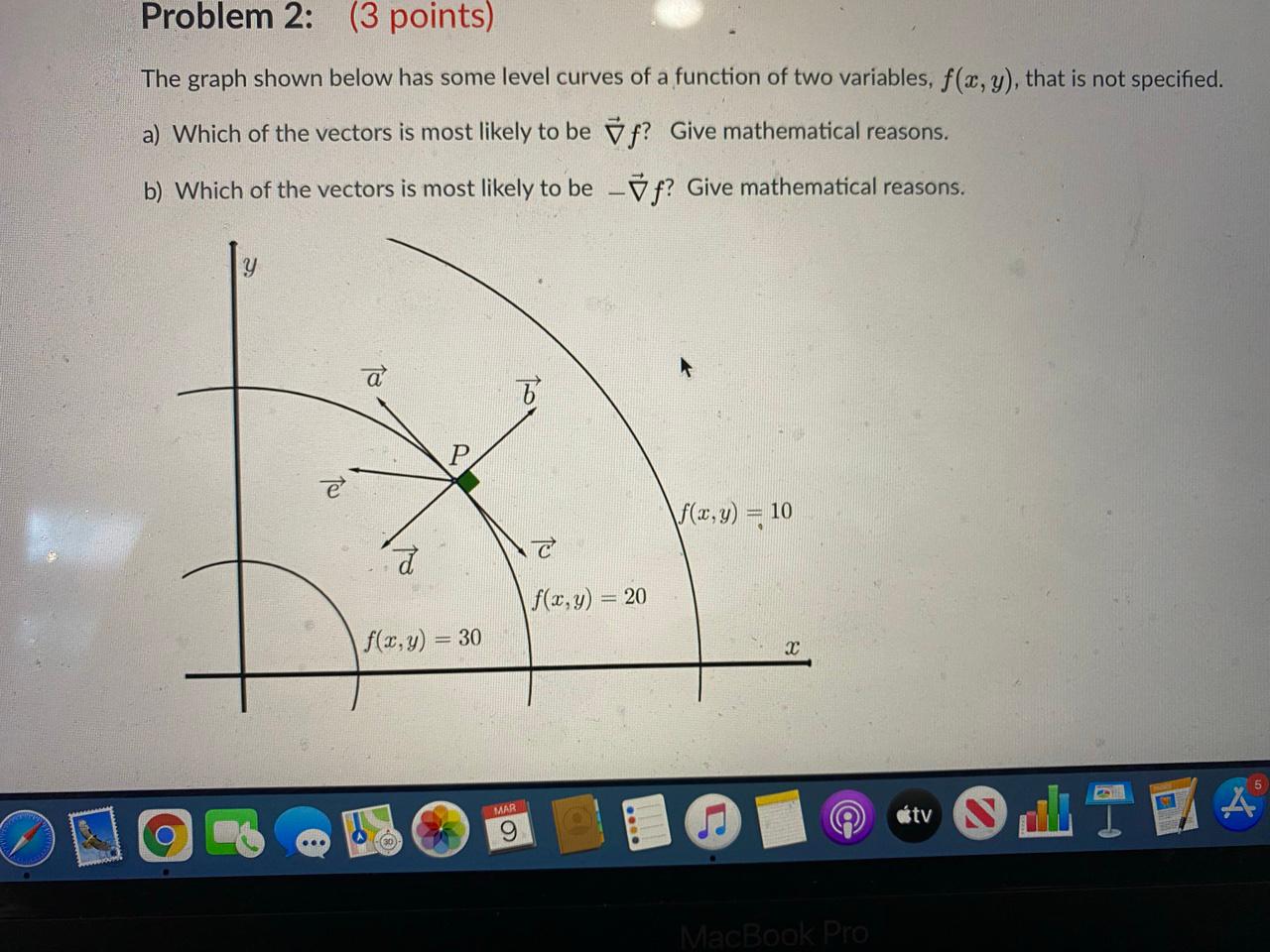



Problem 2 3 Points The Graph Shown Below Has Some Chegg Com




11 Level Curves And Contour Lines Of Functions Of Two Variables Youtube




28 36 38 40 41 15 1 Graphs And Level Curves 927 A Figure 15 18 Section 15 1 Homeworklib




Multivariable Functions And Their Level Curves Dave4math



Level Sets Math Insight



No comments:
Post a Comment